
凯米幼儿数学教育课程
作者:袁贵仁主编 来源:《中国教师新百科》――幼儿教育卷 上传时间:2005-02-18
凯米幼儿数学教育课程(kamii’s mathematics curriculum for young children) 凯米(kamii)等人深受皮亚杰认知发展理论的影响,最大限度地发掘出其中的教育内涵,设计了一套以皮亚杰理论为指导的学前教育课程。虽然与其他皮亚杰课程相比,凯米的课程定型较晚,但被认为是较纯粹的皮亚杰课程。在凯米的课程理论中,关于数学教育方面的内容集中体现在《重新建构孩子的数学能力――皮亚杰理论在数学上的应用》 (Young Children Reinvent Arithmetic:Implication of Piagets Theory)一书中,关于幼儿数学教育的思想主要体现在《第1级:幼稚园―小一》一书中。
理论基础 凯米追随皮亚杰,吸收延伸了皮亚杰的理论,这构成了她的数学教育课程的主要理论基础。
①儿童数概念的获得――皮亚杰的建构主义思想。凯米吸收和发展了皮亚杰关于儿童知识获得的建构主义思想,认为儿童数学概念的获得是在儿童与环境相互作用的过程中,由儿童自身内部建构出来。其中儿童自身的反思、加工和建构尤其重要。
②数理逻辑知识的本质。皮亚杰理论认为儿童的知识包括物理性知识、数理逻辑知识以及社会性知识,这三类知识在课程中占有重要地位是凯米课程的特点之一。她指出皮亚杰确认了知识的内部来源与外部来源,对于个体而言,物理性知识及社会性知识的来源有部分是外部的,而数理逻辑知识的来源则是内部的,是由个体内部建构的关系所组成的。
③数学活动中的表征。凯米指出皮亚杰有关表征的理论与传统经验主义者在数学教育基础上的假设是不同的。传统数学教材中有许多图片,而这些图片的产生是基于如下假设的:孩子数学能力的发展过程是从具体的(物体)到半具体的(图片)以及最后到抽象的(书写数字),这种半具体的图片就是表征。然而根据皮亚杰理论我们可以了解到,这些假设是错误的。儿童数学能力的发展,不是从具体的到半具体的再到抽象概念发展的层级关系。儿童在数学学习过程中不需要任何图片,他们更多是通过操作物体,在感知的基础上,逐渐由外部动作内化为内部的心理活动,在头脑中建构物体之间的数量关系的。因此,表征与抽象化不同,表征是孩子们在头脑内部建构的关于客观事物的形象以及数量关系,表征不是抽象化。
④社会交往(互动)对儿童建构数学能力的重要性。凯米等人批驳了那些认为皮亚杰理论忽视孩子发展过程中社会性因素的观点,指出皮亚杰也非常重视社会交往对儿童发展的重要作用,例如皮亚杰曾说:“与别人交换思想对儿童逻辑的发展以及科学家建构科学概念都是不可或缺的。”因此,在凯米的数学教育思想中,也吸收了皮亚杰的这一观点,充分重视社会交往对儿童数理逻辑知识发展的重要性。
促进儿童自律发展目标 凯米以及皮亚杰主张的教育目标――自律为基础,探讨如何在数学教育过程中促进儿童自律的发展。
皮亚杰认为,自律就是自己管理自己的能力,它是个人在不受奖赏及惩罚的影响下,考虑一些相关因素,在道德领域决定对自律的相反是他律,他律是被别人控制、自己不能做出判断。儿童最初都是他律(0%),不能分辨是非善恶,随后自律逐渐发展。理想状态下,儿童长大时,他们会变得比较自律,相对比较不会他律,直到孩子变得能控制自己时,就不会受其他人的控制了。
图1 道德自律发展理想与实际曲线对照
自律
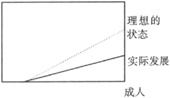
在道德自律方面,成人有时并没有按照理想的曲线(见图1)来发展,很少有成人完全发展出道德自律。有时孩子在道德上比成年人更加自律,皮亚杰指出其中原因在于“当成年人用奖赏的方式对待孩子时,便加强了孩子的他律;而当他们与孩子交换意见看法时,便能刺激孩子自律的发展”。另外,相互尊重对儿童自律的发展是非常重要的,那些感觉被尊重的孩子也比较能尊重其他人的想法及感觉。
智能自律(intellectual autonomy),是指“孩子并不是不动的瓶子,仅仅只会保留放在脑中的事情,他们可以通过创造及协调各种关系来建构一个更加广泛和更深入的知识网络构架”。
凯米认为,现今大部分学校的教育目标只实现了一部分的自律目标,而大部分实现的目标是他律,也即学校大多是用强加的奖赏、惩罚以及已有的规定来教育学生的。学生在学校获得的知识大部分是在考试之后就会忘记的――他律的知识,而仅有少部分是不会忘记的――自律的知识。因此,当我们把道德自律和智能自律作为我们的教育目标时,学校教育必须努力通过相互尊重的讨论以及儿童的去自我中心化,促进儿童从内在心理出发,控制自己的学习和行为,增强儿童的道德和智能自律。
皮亚杰把自律作为教育的目标。凯米以此为基础,认为数学教育的目标也应该是培养儿童的自律,也即通过儿童之间的交流、讨论,使儿童逐渐学会自己做出决定,找到问题解决的方法,发展数理逻辑推理能力。凯米从加、减、乘、除4个方面人手,积极培养儿童在这些数学活动中的自主性和能动性,也即在这些数学活动中努力实现儿童数学教育的目标――儿童自律的发展。
课程内容 主要包括3个方面:①数学活动以外的生活情境中的数学学习。凯米认为数学是由孩子在情境中将其真实的经验数理逻辑化而获得的,因此应该利用数学课之外的情境来丰富幼儿的数学经验。她指出,日常生活中每日、每月或节假日发生的许多事情等都会涉及时间、数字等数学概念,并自然地层开与数学有关的讨论,这些讨论一般不用花费太多时间,同时又能使学生很容易地在日常的情境中觉察和认识数学。比如,将书分类、按数量分配物品、分割物体、累计物品等等,都会提供进行数学推理的良好机会;另外,处理与金钱有关的事情也可以让幼儿从中理解“钱”的用途、钱的多少以及理解和获得用钱9B买东西、买多少东西等概念和经验。②文字题。主要目的是让孩子将真实世界的经验数理逻辑化。凯米指出,“正如我们的祖先是在真实生活的日常需要的基础上创造出数学一样,今天我们的孩子也应该被鼓励在他们的真实生活中进行各种运算”。③专门设计的游戏活动。一些儿童在日常生活情境以及文字题中没能充分发展自身的数学能力,为此,凯米设计专门的数学游戏活动,包括逻辑推理、时空推理、小的数字、数值游戏以及各种加减法的游戏,以帮助这些儿童更加充分地发展他们的数学能力。
教学原则 凯米指出,要实现自律的教育目的,必须要让孩子在讨论相关因素的过程中逐渐学会自己做出决定,这就要求“必须尽可能降低成人的权威作用,让孩子之间彼此交换意见”,学会自己做出决定。而要让孩子之间很容易地交换意见,就要有能够互相体谅和尊重的班级氛围,同时让孩子自己尝试解决问题。
基于上述讨论,凯米指出,“对于数学课上的自律发展而言,最主要的是教师应首先利用孩子的内在动机来促进学习”。教师不要教孩子如何解决问题,而是要先给孩子问题,让他们用自己已知的知识去寻求新的解答问题的方法。为此,教师应该提问题而不是告诉孩子该怎样做;应提出有一定难易差异的问题,并能适当调整问题的难易程度;让每一个孩子都用自己不同的方法解决问题;了解是不是所有的孩子都能够真正自己发现问题的答案和解决的方法。不要告诉孩子问题答案的正确与否,只要每一个孩子都认同一个答案,那么这个答案就是有意义的,因为它是孩子内心建构的数理逻辑关系。那么,会不会出现全班孩子都认同一个不正确的答案呢?此时教师应该怎么办?凯米的回答是:“这样的情况不会发生,即使它真的发生了,老师们也应该了解这个问题对孩子来说一定是太难了。”让儿童在生活情境和文字题中掌握数学知识、学会数学计算。明确游戏中的练习活动优于单纯的练习作业。
除了数学教育的一般原理之外,凯米还特别强调了儿童游戏时的教学原则。她认为,儿童进行数学游戏时,教师如果总是纠正孩子的错误,或是控制孩子的一切活动,那么孩子就无法发展自信及主动。为此,凯米针对教师们经常提出的问题,提出游戏时教师应该掌握的一些教学原则。例如,班级秩序失去控制时教师应该让孩子在讨论过程中自己寻求解决问题的办法;选择游戏时应该根据一定的目标顺序,同时考虑儿童的年龄发展阶段以及每个儿童的数学能力及兴趣;让孩子自己选择想要玩的游戏以及和谁玩;让孩子自己规定游戏规则;孩子游戏时教师最好和每一个孩子或一小组成员一起玩游戏。
凯米认为,由于自己的数学教育目标与以往的传统教法不一样,那么,评价的方式也应该与传统的学业成就测验不同。传统的学业成就测验中,更多将关注点集中在如何尽快得到正确答案,而我们的评价应该是评价孩子的数理逻辑推理能力以及他们对以自己的能力去寻找答案的自信。
课程特点 凯米数学课程继承和发扬了皮亚杰建构主义思想以及皮亚杰对三类知识的划分,强调儿童在与环境的互动过程中建构数理逻辑知识;重视儿童在数学学习过程中自主性、能动性的发挥;强调真实生活情境中的学习,重视利用正式教学活动以外的日常生活情境以及有一定情境的各种文字题来促进儿童的数学学习;重视认知发展与会性发展之间的密切结合,尤其重视社会往、互动对儿童数学学习的重要性;基于亚杰将教育目标定位在儿童自律的发展,凯米主张数学教育的目标也应该是发展儿童自律,让儿童通过与他人相互交换意见,寻找问题解决的办法,以及在自己做出决定过程中发展数理逻辑推理能力;强调数学评价不应仅局限于寻找正确的答案,而应该评价儿童数理逻辑推理能力的发展以及儿童对以自己的能力寻找问题答案的自信。
- 相关博文:
- 幼儿园儿童数学教育的8个途径
 gzmdh406阅读人气:1766
gzmdh406阅读人气:1766 - 教育论坛(发表):浅析幼儿园...
 世外仙姝阅读人气:1396
世外仙姝阅读人气:1396 - 科学教育活动中幼儿尝试精神的...
 低调含香阅读人气:1927
低调含香阅读人气:1927 - 幼儿园与小学教育的断层与衔接
 仙林奇境阅读人气:1601
仙林奇境阅读人气:1601 - 指导家长创设家庭科学教育环境...
 丰台三幼赵燕茹阅读人气:3068
丰台三幼赵燕茹阅读人气:3068
- 幼儿园儿童数学教育的8个途径
- 已回答相关问题:
- [教师工作]幼儿体育课程该怎么开展?
 长颈鹿阅读人气:1369
长颈鹿阅读人气:1369 - [业务管理]如何增加幼儿安全教育课的实效...
 雪阅读人气:1224
雪阅读人气:1224 - [园长管理]如何增加幼儿安全教育课的实效...
 快乐天使阅读人气:1497
快乐天使阅读人气:1497 - [教师工作]幼儿数学区分大小
 哈喽阅读人气:1178
哈喽阅读人气:1178 - [教师工作]中班幼儿老咬人教育多次,还是...
 风儿阅读人气:1162
风儿阅读人气:1162


- [教师工作]幼儿体育课程该怎么开展?






